Product Tear-down Canister Whipped Cream
Overview -
Status: Draft
What better way to introduce thin wall pressure vessels than a canister of whipped cream. My goal in this teardown is to illustrate how designing a canister requires detailed engineering especially for a mass production unit where every cent counts. This teardown includes: 1) hoop stress analysis, 2) failure criteria intro, and 3) preliminary raw material estimate.

Observations
Components
Manufacturing
Flow Path
Analysis
Hoop & Axial Stress
Von Mises Stress
Safety Factor
Discussion
References
Observations
Components
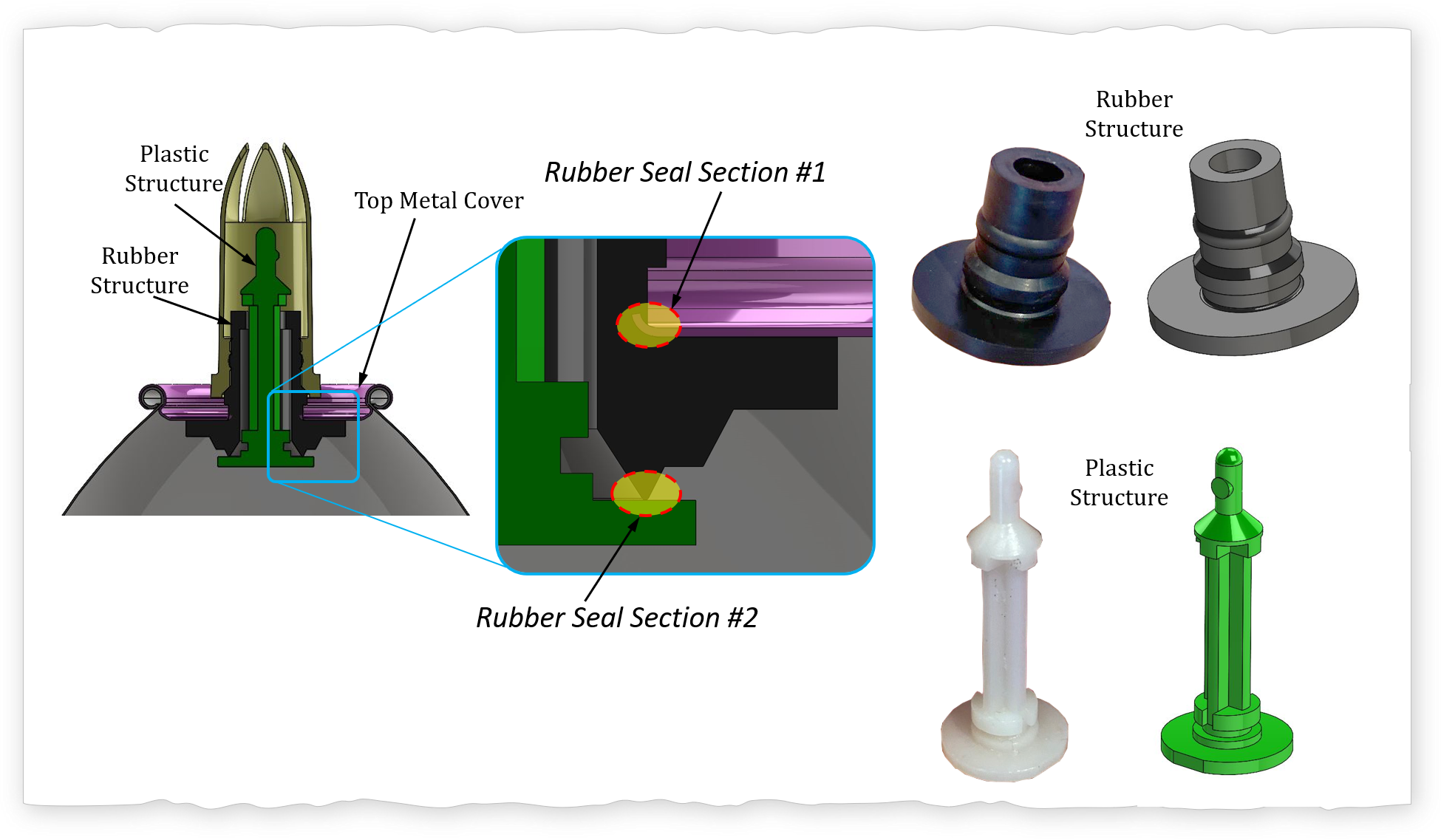
The whipped cream container consist of a total of seven parts, six of which have been modeled in CAD. The cover cap (not shown) is made using injection molding. The dispensing tip and plastic structure are both made from plastic as well. The plastic structure can be made from a two part mold (see manufaturing). A rubber element serves to create the seal between the inside of the canister and the world in conjunction with the plastic structure. There are three metal parts that create the canister: 1) top metal cover, 2) metal shell, and 3) bottom metal cover.
Manufacturing
The three metal parts of the canister are joined by deforming the metal sections areound each other. The internal surface of the canister has a coating which may be assisting to seal the region of the joint. The bottom of the canister is joined using what appears to be a cup joint seam. The top of the canister is joined by beading of both the top metal cover and the metal shell together and deforming internal part of the top metal cover radially radially outwards to prevent axial motion. Can you see the difference between the CAD model and the photo. The CAD model is slightly off in the beaded region. I initially created the CAD without taking the cross section, this is why it is important to go in depth into the details. While it is easy to change, I left it on the CAD model as a learning opportunity.
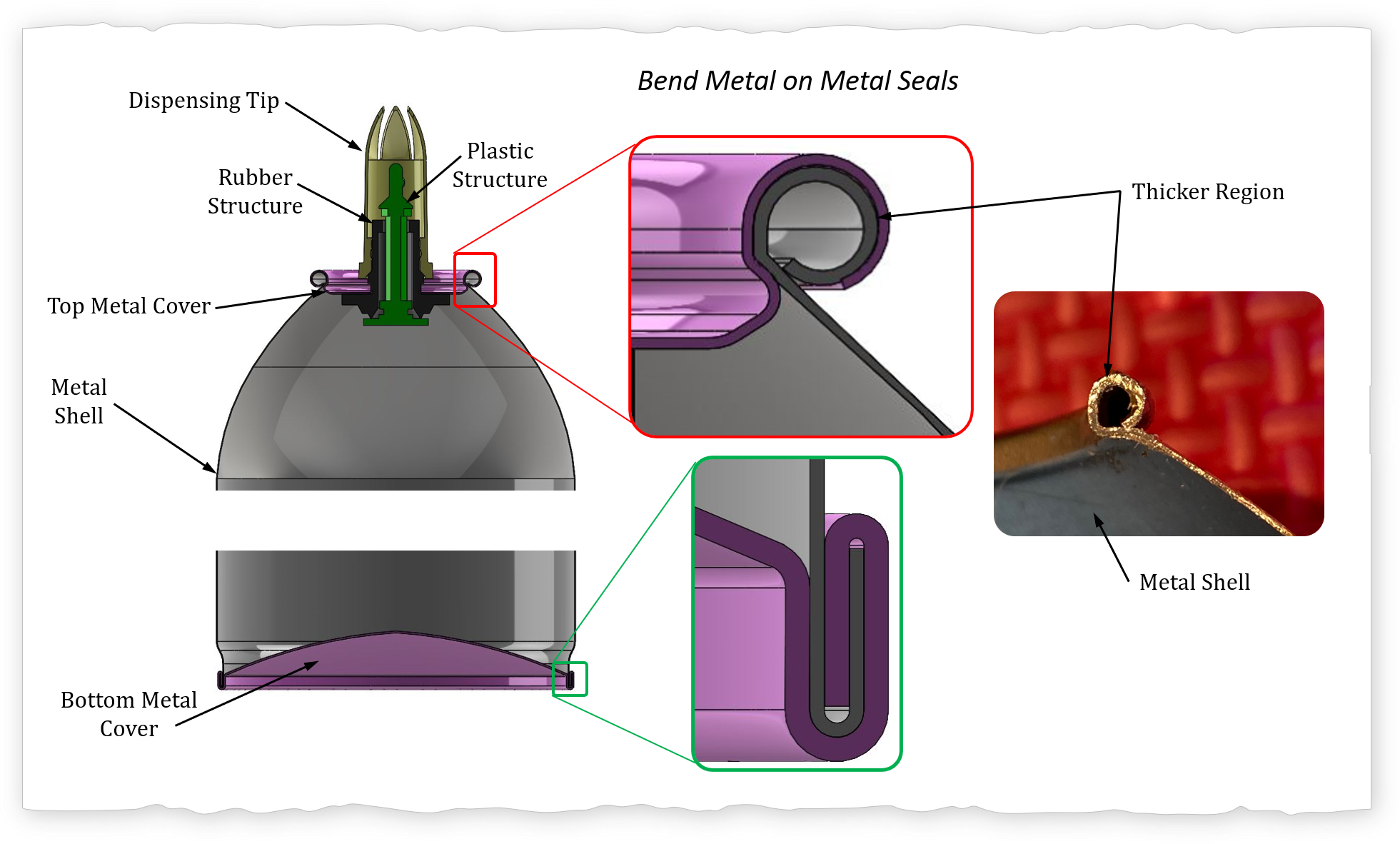
The thicker region of metal shell alludes to how the metal shell was fabricated. The thickness of the beaded area of the metal shell is approxiamtely 0.33 mm. The wall thickness along the cylindrical region is ~ 0.18 mm. I used the CAD model to determine an approximate thickness of the coating in the inside of the canister using a volume comparison. The metal shell was most likely fabricated from a cylinder blank internal diameter (25.4 mm), thickness (0.33 mm), and for comparison I just fixed the height to (h = 170 mm). The metal shell height was fixed to the same as the cylinder. The canister shell geometry thickness was then reduced from 0.18 mm until the volume was equal to that of the cylinder blank. It turns out that when the canister shell wall thickenss is 0.13 mm (coating 0.05 mm) the volume of the cylindrical blank is about equal to that of the metal shell for the same height. Thus, I'm estimating that the coating is approximately 0.05 mm thickness which about half of a hair diameter.

Seal
The rubber structure creates two seal interfaces. The first seal interface is between teh rubber and the top metal cover. The aperture (opening) of the metal is smaller than the outer diameter of the rubber section in that region thus there is an interference fit. The squezing of the rubber element by the metal creates a seal. The metal section is slightly tapered upwards to mitigate the rough surface from shearing affecting the sealing interface (see shearing section). The second rubber seal is between the plastic structure and the rubber. The internal pressure inside the canister pushes the plastic structure axially upwards towards the rubber element. The higher the pressure the better the seal, this can be considered a self-help principle.
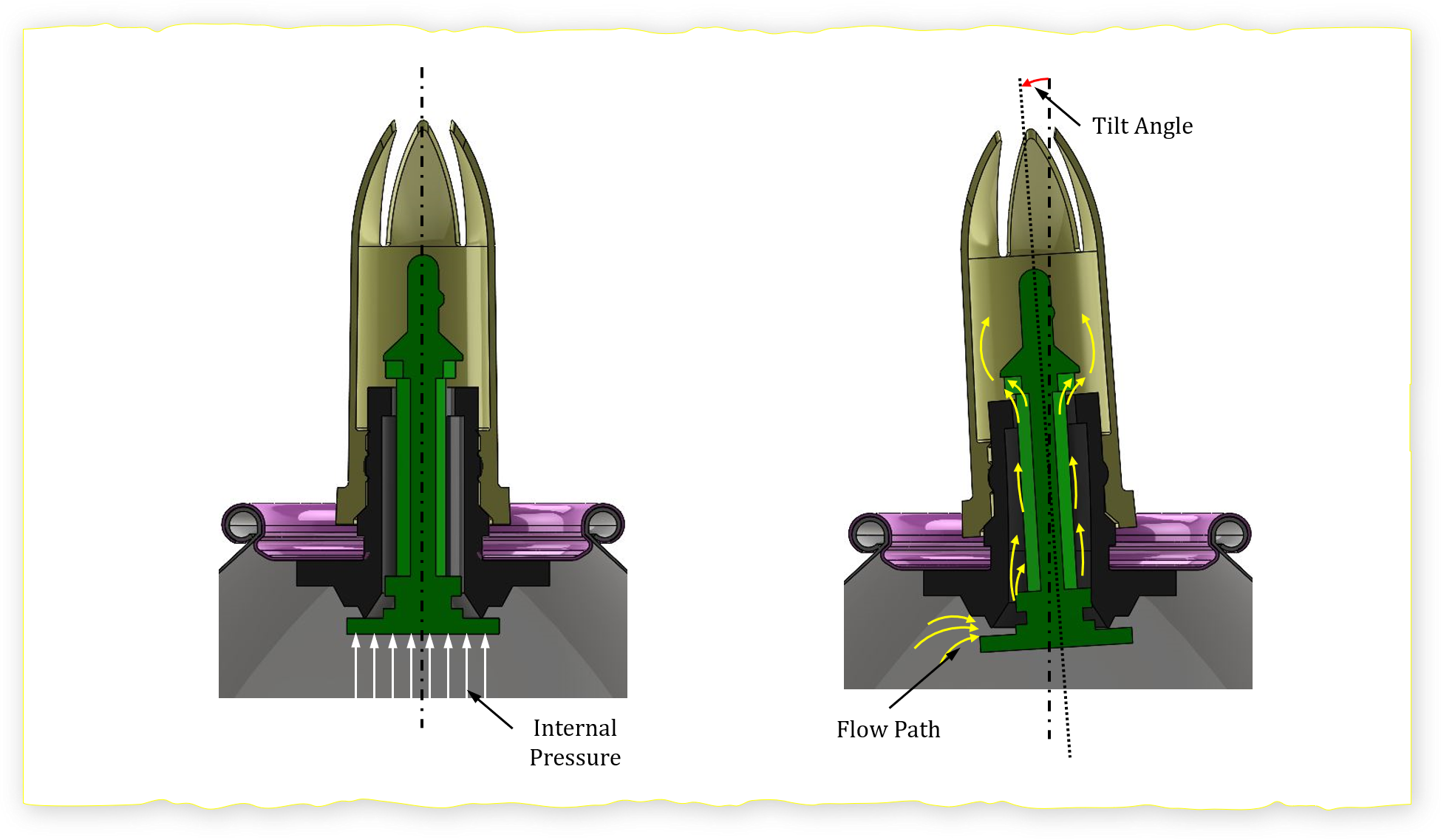
Flow Path
The tilting of the dispensing tip creates a deformation in the rubber structure and a tilting of the plastic structure (green) breaks the seal allowing for the fluid to exit the canister.
Analysis
Our goal is going to relate the loading (aka pressurized canister) to the material properties to estimate the safety factor (\( \eta \)) for the hoop stress (tangential stress) of the canister.
Cylinder Hoop and Axial Stress
The wonderful thing about some equations is that they are extremely easy to derive. The hoop (tangential) and axial (longitudinal) stress for thin wall cylinders can be quickly derived by simply setting up the equilibrium equation. You can find the detailed in Section 2A1 - Pressure Vessels & Piping (Link coming soon).
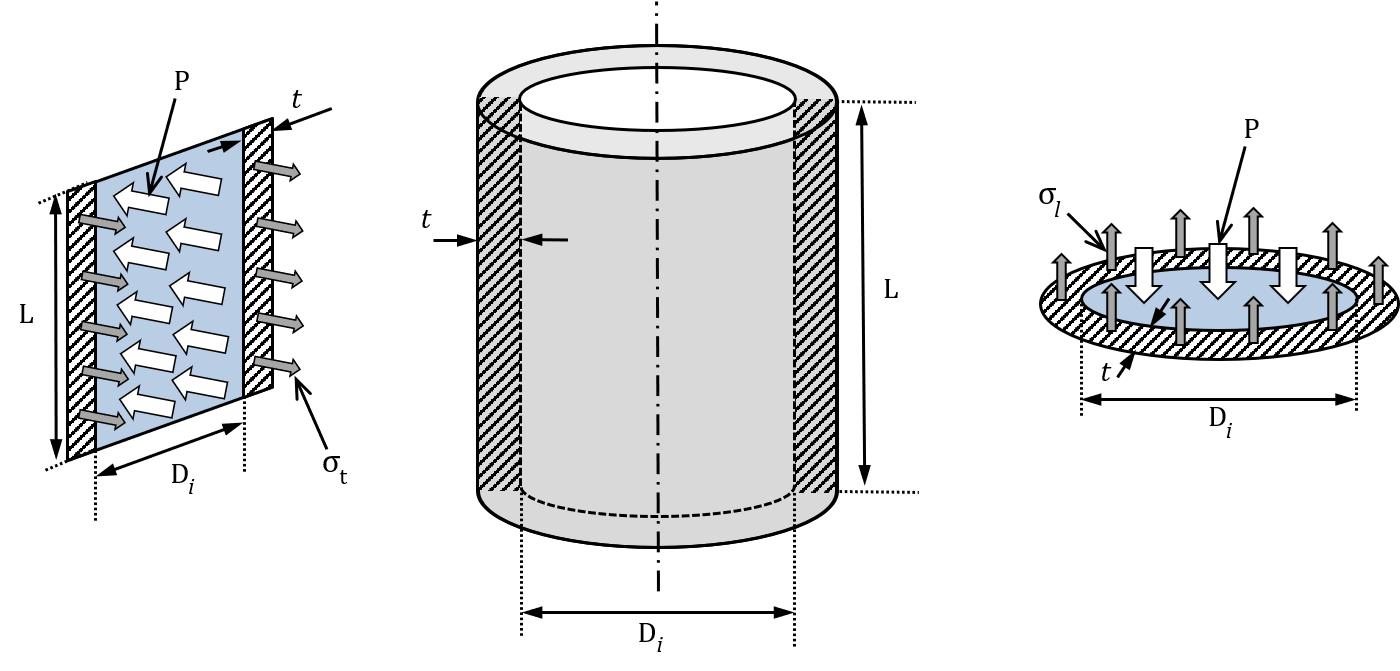
Hoop or Tangential Stress
$$ \sigma_{_t} \cdot 2 \cdot t \cdot L = P \cdot D_i \cdot L $$ $$ \sigma_{_t} = \frac{P \cdot D_i}{2 \cdot t} = \sigma_{_\theta}$$Axial or Longitudinal Stress
$$ \sigma_{_l} \cdot \frac {\pi \cdot D_i^2}{4} = P \cdot D_i \cdot t $$ $$ \sigma_{_l} = \frac{P \cdot D_i}{4 \cdot t} = \sigma_{_a}$$Loading ⇒ Material Properties & von Mises
The relationship between loading and the yield stress (\( \sigma_y\) ) is failure criteria. Now let's jump in head first... If you were to only pick up one piece of knowledge from this example it should be: von Mises Stress. Please note: ** This is only an introduction to the subject (aka tip of the iceberg) and a first order analysis. ** There are several other factors that can affect this analysis such as: temperature, fatigue, corrosion, embrittlement, manufacturing, etc. While the von Mises equation looks complex it will simply very quickly especially when considering that it is just composed of the axial stresses and the shear streeses. Way easier to look at the color diagram.
$$ \sigma_{_{VM}} = \sqrt { \frac {\left( \sigma_{xx} - \sigma_{yy} \right)^2 + \left( \sigma_{yy} - \sigma_{zz} \right)^2 + \left( \sigma_{zz} - \sigma_{xx} \right)^2 + 6 \left( \tau_{xy}^2 + \tau_{yz}^2 + \tau_{xz}^2 \right ) }{2} } $$Axial Stresses
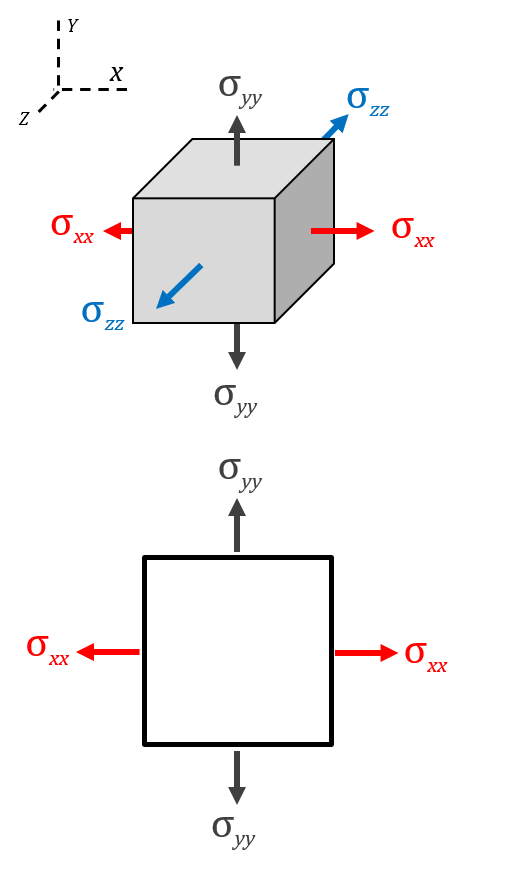
Shear Stresses
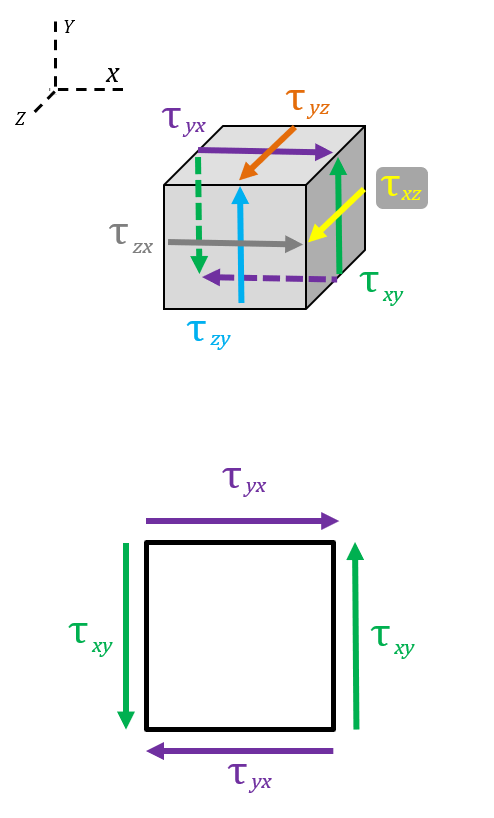
Now we can start cleaning up. What you will notice is that some shear terms are "not in the von Mises stress." Since we are assuming that the system is in static equilibrium, then \( \tau_{xy} = \tau_{yx} \) , \( \tau_{yz} = \tau_{zy} \) , and \( \tau_{xz} = \tau_{zx} \). Thus, the three axial terms and the three shear terms are properly represented in the von Mises stress equation.
For this specific problem we are just going to look at the hoop stress only. Thus, we are assuming that the shear stresses are negligible (section below covers assumptions: depth of geekiness), and that the system is essentially in uniaxial tension. Thus \( \sigma_{_\theta} = \sigma_{_{VM}} = \sigma_{yield}\), where the \(\sigma_{yield} \) is the maximum engineering yield stress of the material (aka a material property). Internal thought: (WAIT! WHAT! So why write down that big equation on top!) Rational: It is important to know that there is more beyond the surface. Thus, we arrive at the equation below that includes the safety factor \( \eta \).
$$ \sigma_{_\theta} = \frac{P \cdot D_i}{2 \cdot t} = \sigma_{operating} = \frac{\sigma_{_{VM}}}{\eta} = \frac{\sigma_{_{yield}}}{\eta}$$We now can relate the loading (internal pressure \(P\) ), geometry (internal diameter \(D_i\), thickness \(t\)), and design considerations (safety factor \(\eta\)) to the intrinsic property material yield stress \( \sigma_{yield}\). Note that what is important is the differential pressure between the inside of the canister and the outside, thus \( \Delta P\). Always try to check units at the end of shuffling equation, typos can happen.
$$ \eta = \frac{ 2 \cdot \sigma_{_{yield}} \cdot t}{\Delta P_{max} \cdot D_i}$$Estimate Safety Factor \( \eta \)
I went online and try to look for the loading of the internal pressure of the whipped cream cannister and could not get a concrete number. Estimate vary between 30 psi to 50 psi. NOTE that all analysis is done in metric units! I convert to metric as a default. Now we use the estimate thickness of t = 0.13 mm to be conservative, otherwise using t = 0.18 mm would be inaccurate since it would over estimate the thickness of the steel and I'm assuming that the coating does NOT have the same strength of the base steel material. The internal diameter of the canister is set to \( D_i = 65.98 mm \). Below is a thin wall pressure vessel spreadsheet as well as two tables with safety factors calculated.
Aluminum \( \sigma_y = 69 MPa\)
Thickness |
30 psi 207 kPa |
50 psi 345 kPa |
|---|---|---|
\( t=0.13mm \) |
1.81 |
1.09 |
\( t= 0.18mm \) |
2.51 |
1.50 |
Steel \( \sigma_y = 250 MPa\)
Thickness |
30 psi 207 kPa |
50 psi 345 kPa |
|---|---|---|
\( t=0.13mm \) |
4.76 |
2.86 |
\( t= 0.18mm \) |
6.59 |
3.96 |
Discussion
Now consider if you were asked to do a raw material cost analysis to determine if you should keep making the cannister out of steel or change it to aluminum while keeping the same safety factor of the original canister. How much would the new canister weight compare to the original?
Journey to the Depths of Geekiness
Each assumption has implications. One duty of an engineer can be determine the validity of those assumptions based on the boundary conditions (aka parameters), and quantify the implications. Here are some open ended questions to consider:
→ Limitations of a thin wall pressure vessel model and assumptions for which it is valid?
→ What are the assumptions that we are making about the 0.05 mm coating thick surface?
→ What are the boundary conditions at the coating steel interface?
→ What happens at the edgest of the container when the radial stress meets the longitudinal stress?
→ What is the change in diameter of the canister as a function of internal pressure.
References
Thin Pressure Vessel
Von Mises
DARE2MAKE CHALLENGE
Find Your Passion
Invest in Education & Growth
Make Something Amazing
Schedule
- Overview Meche PE
- Product Dev. Process
- Explore → Hands On
- I - Principles
- → Foundation
- → A - Basic Engineering Practices
- → B - Engineering Science and Mechanics
- → C - Material Properties
- → D - Strength of Materials
- → E - Vibration
- II - Applications
- → A - Mechanical Components
- → B - Joints and Fasteners
- → C - Supportive Knowledge
- III - Holistic Knowledge
- → A - Heat Transfer
- → B - Fluid Dynamics
- → C - Controls
- → D - Thermodynamics
- → E - Electronics
- IIII - Precision Machine
- → A - Error Apportionment
- → B - Metrology